Skip to main content

Using PCA in MDP


I found mdp on sourceforge. I needed to do PCA for some of my simulations. The mdp.pca function is easy to handle. The input is a m x n matrix, n is the dimension of the space, and m are the observations (rows = observations, cols = dimensions. The doc string is confused as to this point)

The output is a matrix also m x n, but the vectors have been transformed, so that the first column is along the direction with greatest variance etc.

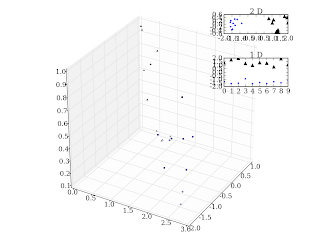
An example is below:


import pylab as m
import matplotlib.axes3d as m3
import mdp

x1 = m.rand(10,3)
x2 = m.rand(10,3) + m.array([[2.,-2.,0.]])
x = m.concatenate((x1,x2))
y = mdp.pca(x)

fig = m.figure()
ax = m3.Axes3D(fig)
ax.scatter3D(x[:10,0].squeeze().T, x[:10,1].squeeze().T, x[:10,2].squeeze().T, marker = '^')
ax.scatter3D(x[10:,0].squeeze().T, x[10:,1].squeeze().T, x[10:,2].squeeze().T, marker = 'o')
m.axis('scaled')
m.axes([.7, .8, .2, .2])
m.plot(y[:10,0], y[:10,1],'k^')
m.plot(y[10:,0], y[10:,1],'b.')
m.axis('scaled')
m.title('2 D')

m.axes([.7, .6, .2, .2])
m.plot(y[:10,0],'k^')
m.plot(y[10:,0],'b.')
m.axis('scaled')
m.title('1 D')
Labels:

Comments

  1. Simon HearneAugust 9, 2010 at 11:57 AM

    For anyone reading this, the code needs to be updated for the latest version of matplotlib:
    line 2 should be:
    import mpl_toolkits.mplot3d as m3

    also add m.show() at the end to display the results.

    ReplyDelete

Post a Comment

Popular posts from this blog

A note on Python's __exit__() and errors

Python's context managers are a very neat way of handling code that needs a teardown once you are done. Python objects have do have a destructor method ( __del__ ) called right before the last instance of the object is about to be destroyed. You can do a teardown there. However there is a lot of fine print to the __del__ method. A cleaner way of doing tear-downs is through Python's context manager , manifested as the with keyword. class CrushMe: def __init__(self): self.f = open('test.txt', 'w') def foo(self, a, b): self.f.write(str(a - b)) def __enter__(self): return self def __exit__(self, exc_type, exc_val, exc_tb): self.f.close() return True with CrushMe() as c: c.foo(2, 3) One thing that is important, and that got me just now, is error handling. I made the mistake of ignoring all those 'junk' arguments ( exc_type, exc_val, exc_tb ). I just skimmed the docs and what popped out is that you need to return True or
Post a Comment
Read more

Store numpy arrays in sqlite

Use numpy.getbuffer (or sqlite3.Binary ) in combination with numpy.frombuffer to lug numpy data in and out of the sqlite3 database: import sqlite3, numpy r1d = numpy.random.randn(10) con = sqlite3.connect(':memory:') con.execute("CREATE TABLE eye(id INTEGER PRIMARY KEY, desc TEXT, data BLOB)") con.execute("INSERT INTO eye(desc,data) VALUES(?,?)", ("1d", sqlite3.Binary(r1d))) con.execute("INSERT INTO eye(desc,data) VALUES(?,?)", ("1d", numpy.getbuffer(r1d))) res = con.execute("SELECT * FROM eye").fetchall() con.close() #res -> #[(1, u'1d', <read-write buffer ptr 0x10371b220, size 80 at 0x10371b1e0>), # (2, u'1d', <read-write buffer ptr 0x10371b190, size 80 at 0x10371b150>)] print r1d - numpy.frombuffer(res[0][2]) #->[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] print r1d - numpy.frombuffer(res[1][2]) #->[ 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.] Note that for work where data ty
Post a Comment
Read more